Rewriting Type Theory
SPLS 2020
Jesper Cockx, Nicolas Tabareau, and Théo Winterhalter
21 October 2020
Introduction
Extending Martin-Löf Type Theory
- Formation rules: \(\quad\)
Bool : Type - Introduction rules: \(\quad\)
true false : Bool - Elimination rules:
ifpt : P trueandpf : P false
thenif b then pt else pf : P b - Computation rules:
if true then pt else pf ↝ pt
Restrictions imposed by proof assistants
- Strict positivity
- Coverage of pattern matching
- Structural recursion
Required to ensure soundness, type preservation, and effective typechecking!
Drawing outside the lines
What if this is not enough?
- Option 1: use
postulate - Option 2: hack the language
- Option 3: use a language with rewrite rules
Rewrite rules in Agda
Using rewrite rules in three simple steps
-- 1. Enable rewriting and import primitives: {-# OPTIONS --rewriting #-} open import Agda.Primitive renaming (Set to Type) open import Agda.Builtin.Equality open import Agda.Builtin.Equality.Rewrite -- 2. Postulate some things: postulate id : {A : Set} → A → A id-comp : ∀ {A} {x : A} → id x ≡ x -- 3. Register the rewrite rule: {-# REWRITE id-comp #-}
Definitional equality is fragile
data Vec (A : Set) : Nat → Set where [] : Vec A 0 _∷_ : A → Vec A n → Vec A (suc n)
rev : Vec A n → Vec A n rev xs = rev-acc xs [] where rev-acc : Vec A n → Vec A m → Vec A (m + n) rev-acc [] ys = {! ys !} -- ^ Error: m != m + 0 rev-acc (x ∷ xs) ys = {! rev-acc xs (x ∷ ys)!} -- ^ Error: suc (m + n) != m + (suc n)
Rewrite rules to the rescue!
+zero : m + 0 ≡ m +zero = ⋯ +suc : m + (suc n) ≡ suc (m + n) +suc = ⋯ {-# REWRITE +zero +suc #-} rev-acc : Vec A n → Vec A m → Vec A (m + n) rev-acc [] ys = ys rev-acc (x ∷ xs) ys = rev-acc xs (x ∷ ys)
HITs that compute
postulate S¹ : Type base : S¹ loop : base ≡ base module _ (P : S¹ -> Set) (pbase : P base) (ploop : pbase ≡ pbase [ P ↓ loop ]) where postulate elim-S¹ : (x : S¹) -> P x elim-S¹-base : elim-S¹ base ≡ pbase {-# REWRITE elim-S¹-base #-} postulate elim-S¹-loop : apd elim-S¹ loop ≡ ploop {-# REWRITE elim-S¹-loop #-}
Defining quotient types
postulate _//_ : (A : Set) (R : A → A → Prop) → Set proj : A → A // R quot : ∀ x y → R x y → proj x ≐ proj y ∈ A // R //-rec : (f : A → B) → (q : ∀ x y → R x y → f x ≐ f y) → (x : A // R) → B //-beta : (f : A → B) → (q : ∀ x y → R x y → f x ≐ f y) → (x : A) → //-rec f q (proj x) ≡ f x {-# REWRITE //-beta #-}
Extending type theory with rewrite rules
The sledgehammer of equality reflection
\[ \frac{\Gamma \vdash e : x =_A y}{\Gamma \vdash x \equiv y} \]
But when to apply this rule?
Typechecking becomes not just undecidable, but also completely unfeasible in practice.
Instead we mark specific equalities as rewrite rules that can be applied automatically!
Rewrite rules, in general
Any equality of the form \[ eq : ∀\ x₁\ …\ xₖ → f\ p₁\ …\ pₙ ≡ v \] can be used as a rewrite rule, provided:
- \(p₁ … pₙ\) are patterns
- \(p₁ … pₙ\) are linear in \(x₁ … xₖ\)
- \(f\ p₁\ …\ pₙ\) and \(v\) have the same type
- \(f\ p₁\ …\ pₙ\) does not reduce
Higher-order patterns
Patterns can be higher order Miller patterns:
postulate rew₁ : f (λ x → x) ≡ t₂ rew₂ : ∀ (y : T) → f (λ x → y) ≡ y rew₃ : ∀ (q : T → T) → f (λ x → q x) ≡ q t₃ rew₄ : ∀ (y : T) → h (λ (p : T → T) → p y) ≡ y {-# REWRITE rew₁ rew₂ rew₃ rew₄ #-}
Miller fragment: Each pattern variable must be applied to distinct bound variables
Other extensions of rewriting
- Non-linear rewrite rules
- Rewriting modulo \(η\)-equality
- Rewriting modulo irrelevance
- Rewriting in parametrized modules
- Rewriting universe-polymorphic functions
- Rewriting in presence of metavariables
Taming your rewrite rules
Rewrite rules are great! But what about…
- … logical soundness?
- … decidable typechecking?
- … type preservation?
Logical soundness
A rewrite rule 0 ↝ 1 breaks soundness!
… but that’s no different from using postulate.
Theorem. If all rewrite rules are provable, then soundness is preserved.
Proof. By translation to extensional type theory.
Termination
A rewrite rule loop ↝ loop breaks termination!
… but termination is not a critical property.
Theorem. When the usual conversion algorithm terminates, its answer is still correct.
Proof. Computing the weak-head normal form preserves definitional equality.
Type preservation
A rewrite rule true ↝ 42 breaks subject reduction…
and this is actually a serious problem!
We can limit rewriting to homogeneous rules, but is that enough?
Breaking type safety by rewriting function types
postulate rew : Nat → Nat ≡ Nat → Bool
{-# REWRITE rew #-}
0' : Bool
0' = (λ (x : Nat) → x) 0
test : Nat
test = if 0' then 42 else 9000 -- Uh oh...Breaking type safety by rewriting type constructors
record Box (A : Set) : Set where
constructor box
field unbox : A
open Box
postulate rew : Box (Nat → Nat) ≡ Box (Nat → Bool)
{-# REWRITE rew #-}
0' : Bool
0' = unbox {Nat → Bool} (box {Nat → Nat} id) 0
test : Nat
test = if 0' then 42 else 9000 -- Uh oh...Breaking type safety with non-confluence
postulate
X : Set
rew₁ : X ≡ Nat → Nat
rew₂ : X ≡ Nat → Bool
{-# REWRITE rew₁ rew₂ #-}
test : Nat
test = if 0' then 42 else 9000 -- Uh oh...Again we have Nat → Nat == Nat → Bool!
Three requirements to ensure subject reduction:
- Rewrite rules should preserve typing
- No rewriting of type constructors
- Rewrite rules + β-reduction should be confluent
Checking confluence
Two problems:
- Checking local confluence is not enough
- Checking termination first is not possible
⇒ standard criterion on critical pairs fails!
We need a stronger property: the triangle property of parallel reduction as used by Tait and Martin-Löf
Parallel reduction
Parallel reduction \(⇛\) reduces all redexes in one step:
\[↝ \ ⊆\ ⇛\ ⊆\ ↝^*\]


The triangle property
Triangle property: each \(t\) has a best reduct \(ρ(t)\)
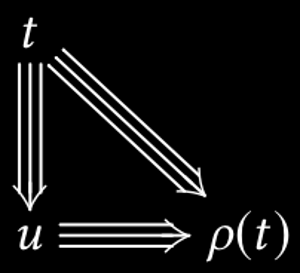
Checking confluence with the triangle property:
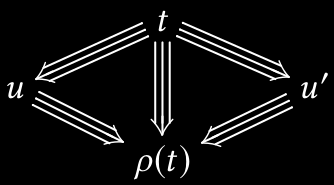
The --confluence-check flag in Agda:
- 2.6.1: local confluence using critical pairs
- 2.6.2: global confluence using triangle property
Conclusion
Rewrite rules are great!
Two categories of use cases for rewrite rules:
- Make more terms typecheck by turning propositional equalities into definitional ones
- Define new primitives that go beyond standard MLTT and make them compute
The triangle property can ensure rewrite rules preserve subject reduction!
Further reading
- Agda documentation:
agda.readthedocs.io - TYPES paper on rewriting in Agda:
https://doi.org/10.4230/LIPIcs.TYPES.2019.2 - POPL paper on safety of rewrite rules:
https://hal.archives-ouvertes.fr/hal-02901011 - Formalization in MetaCoq:
https://github.com/TheoWinterhalter/template-coq/
Ask me questions!
What do you want to hear more about:
- More examples?
- More details on RTT and its formalization?
- More detail of implementation of rewrite rules and confluence check?